神经网络 | 感知器原理及python代码实现and和or函数

目录

感知器原理

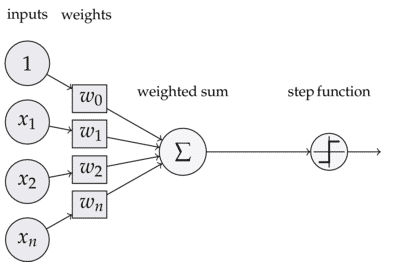感知器结构

如图，感知器中每个输入都有对应的权重，感知器在预测时：

输入向量

$$ \vec{inputs}=(x_1,x_2,...,x_n) $$

输出带权和

$$ weight\_sum=w_0+x_1×w_1+x_2×w_2+...+x_n×w_n=w_0+\sum_{i=1}^n (x_i×w_i) $$

其中即偏置bias
​

令权重也为一个向量，即weights，记为w，则带权和可写为：

$$ weighted\_sum=w_0+\vec{inputs}·\vec{w} $$

最后的输出结果只需把带权和放入激活函数即可：

$$ output=f(weighted\_sum)=f(w_0+\vec{inputs}·\vec{w}) $$

激活函数有很多，例如一些阶跃函数，tanh函数，sigmoid函数等等
​

那么训练模型时就得想办法确定权重向量weights和偏置数bias，具体见如下代码方法和步骤
​

代码方法和步骤

一、感知器代码原理解析

1.训练感知器，通过Perceptron类中的train(self, input_vecs, labels, iteration, rate)方法。

其中input_vecs为输入训练向量，labels为输入训练向量的标签向量，iteration为迭代次数，rate为学习率。每次迭代执行一次_one_iteration(self, input_vecs, labels, rate)，可以理解为一个Epoch。

2.一次迭代中，将输入向量和标签用zip()函数打包在一起成为一个zip object，例如：
[([1, 1], 1), ([0, 0], 0), ([1, 0], 1), ([0, 1], 1)]

对其中的每个(input_vec,label)，调用模型的predict()预测输入input_vec的output，再调用模型的_update_weights(input_vec, output, label, rate)更新输入向量对应的权重和模型整体的偏置bias。

3.权重向量w0初始为[0.0]*维度(在与或函数中维度为2即w0初始为[0.0,0.0] )，在_update_weights()函数中，首先计算出此次迭代的损失值deltak= label – output，即标签和预测值之差，不失为一个朴素的损失函数；再对权重向量weights(记为w)做如下处理：（学习率rate记为r）

对于输入向量集input_vecs中的每一个向量$input\_vec_k$：
VectorOp.element_add(self.weights, VectorOp.scala_multiply(input_vec, rate * delta))

$$ \vec{w_k}=\vec{w_{k-1}}+\vec{input_k}×(r×δ_k ) ,k=1,2,…,n $$

其中n为迭代次数iteration

4.模型预测函数predict(input_vec)传入一个输入向量input_vec，令 input_vec点乘模型权重weights再加上模型偏置bias，如下：
VectorOp.dot(input_vec, self.weights) + self.bias

得到的值传入模型的激活函数activator(x)，本次模型使用的激活函数为一个阶跃函数：

$$ f(x)=\left\{ \begin{array}{rcl} 1& \text{for}& x>0 \\ 0 & \text{for} & x<=0 \end{array}\right. $$

最后激活函数返回的值作为这次predict(input_vec)的返回值返回。

$$ f(V_i \cdot W + Bias) $$

二、训练感知器实现or函数

1. 代码

from __future__ import print_function
from functools import reduce

class VectorOp(object):

    @staticmethod
    def dot(x, y):
        return reduce(lambda a, b: a + b, VectorOp.element_multiply(x, y), 0.0)

    @staticmethod
    def element_multiply(x, y):
        return list(map(lambda x_y: x_y[0] * x_y[1], zip(x, y)))

    @staticmethod
    def element_add(x, y):
        return list(map(lambda x_y: x_y[0] + x_y[1], zip(x, y))) #lambda 即匿名函数


    @staticmethod
    def scala_multiply(v, s):
        return map(lambda e: e * s, v)

class Perceptron(object):
    def __init__(self, input_num, activator):
        self.activator = activator
        self.weights = [-1.0] * input_num # 初始化权重
        print("init weights")
        print(self.weights)
        self.bias = 0.0

    def __str__(self):
        return 'weights\t:%s\nbias\t:%f\n' % (self.weights, self.bias)

    def train(self, input_vecs, labels, iteration, rate):
        for i in range(iteration):
            self._one_iteration(input_vecs, labels, rate)

    def _one_iteration(self, input_vecs, labels, rate):
        samples = zip(input_vecs, labels)
        # print(list(samples))
        for (input_vec, label) in samples:
            output = self.predict(input_vec)
            self._update_weights(input_vec, output, label, rate)

    def _update_weights(self, input_vec, output, label, rate):
        delta = label - output
        #print("=============\ndelta=%.1f"%delta)
        #print("updating,VectorOp.scala_multiply(input_vec, rate * delta):")
        #print(list(VectorOp.scala_multiply(input_vec, rate * delta)))
        #print("\nVectorOp.element_add(self.weights, VectorOp.scala_multiply(input_vec, rate * delta)):")
        #print(list(VectorOp.element_add(self.weights, VectorOp.scala_multiply(input_vec, rate * delta))))

        self.weights = VectorOp.element_add(
            self.weights, VectorOp.scala_multiply(input_vec, rate * delta))
        self.bias += rate * delta

    def predict(self, input_vec):
        return self.activator(
            VectorOp.dot(input_vec, self.weights) + self.bias)


def f(x):
    return 1 if x > 0 else 0

def get_training_dataset():
    # and函数的输入训练向量
    input_vecs = [[1, 1], [0, 0], [1, 0], [0, 1]]
    labels = [1, 0, 0, 0]

    return input_vecs, labels

def get_or_training_dataset():
    # or函数的输入训练向量
    input_vecs = [[1, 1], [0, 0], [1, 0], [0, 1]]
    labels = [1, 0, 1, 1]

    return input_vecs, labels

def train_and_perception():
    p = Perceptron(2, f)
    input_vecs, labels = get_training_dataset()
    p.train(input_vecs, labels, 10, 0.1)
    return p

def train_or_perception():
    p = Perceptron(2, f)
    input_vecs, labels = get_or_training_dataset()
    p.train(input_vecs, labels,0, 0.1)  # 输入向量，标签，迭代次数，学习率
    return p

if __name__ == '__main__':
    #and_perception = train_and_perception()
    #print(and_perception)
    # and测试
    #print( '1 and 1 = %d' % and_perception.predict([1, 1]))
    #print( '1 and 0 = %d' % and_perception.predict([1, 0]))
    #print( '0 and 1 = %d' % and_perception.predict([0, 1]))
    #print( '0 and 0 = %d' % and_perception.predict([0, 0]))

    or_perception = train_or_perception()
    print(or_perception)
    # or测试
    print('1 or 1 = %d' % or_perception.predict([1, 1]))
    print('1 or 0 = %d' % or_perception.predict([1, 0]))
    print('0 or 1 = %d' % or_perception.predict([0, 1]))
    print('0 or 0 = %d' % or_perception.predict([0, 0]))

2. 不同迭代次数和初始权重下的准确率

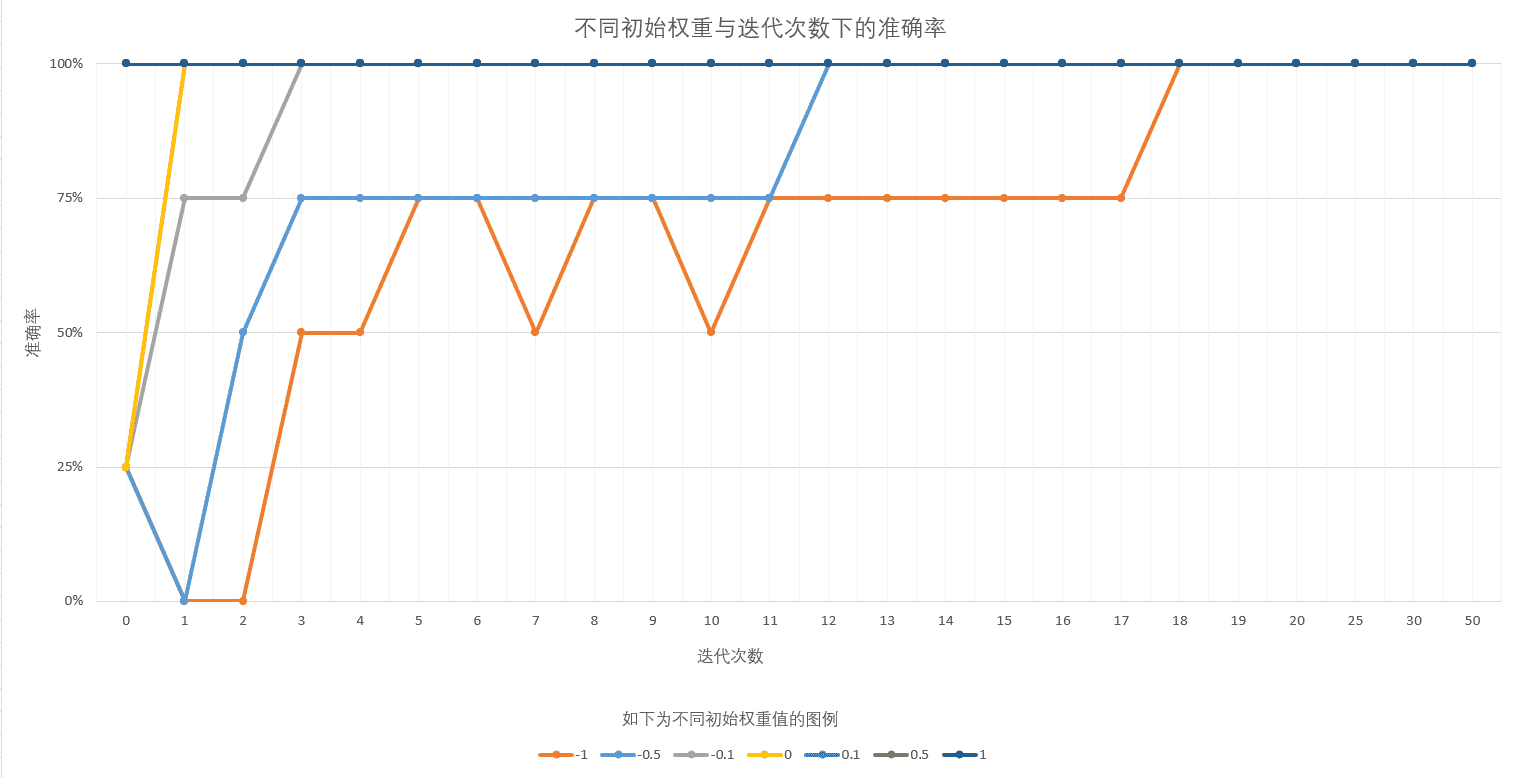不同迭代次数和初始权重下的准确率