编译原理 | 期末复习笔记

作者： 分类：笔记 字数：9460
warning: 这篇文章距离上次修改已过809天，其中的内容可能已经有所变动。

目录


第一章 概论

1. 1 编译过程及程序结构

  • 编译程序：把一种高级语言等价地转换为另一种低级语言（汇编、机器码），共有六个阶段，八个部分。

    • 阶段

      • 词法分析：对源程序从左到右逐字符读入，线性扫描和分解，识别出一个个单词
      • 语法分析：根据语言的语法规则，确定整个输入串是否是语法上正确的程序
      • 语义分析：审查源程序有无语义错误，为代码生成阶段手机类型信息
      • 中间代码生成​
      • 代码优化​
      • 目标代码生成

    • 额外两个部分

      • 符号表管理程序
      • 出错处理程序
  • 翻译程序：边解释边执行，不生成目标代码，仅有编译程序的前三个阶段：词法、语法、语义分析

  • 编译前后端：

    • 编译前端：与源语言有关，如词法分析、语法分析、语义分析、与目标机无关的代码优化等与机器无关的事务
    • 编译前端：与目标机器有关，如目标代码生成、与目标机有关的代码优化
    • 好处：可组装、省力、有利于移植

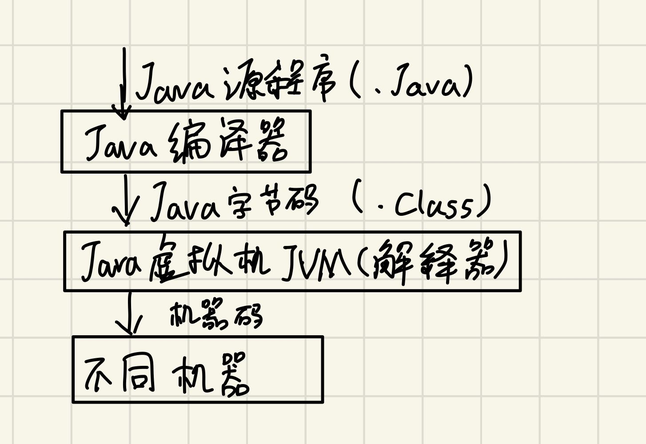
  • Java语言环境

    • BYTECODE（字节码）：需经由JVM才可在目标机器上运行

    • 两种二次处理

      • 解释程序
      • 即时编译程序
    • 运行流程

第二章 文法和语言

  • 文法：G[S] 定义为四元组 $(V_N,V_T,P,S)$

    • $V_N$：非终结符集
    • $V_T$：终结符集
    • $P$：产生式集
    • $S$：开始符（识别符）

  • 文法分类

    • 0型文法（短语文法）
    • 1型文法（上下文有关文法）

    • 2型文法（上下文无关文法）

      • 形如$ \alpha \rightarrow \beta, \alpha \in V_N ;\beta \in (V_N \cup V_T)^* $，也即左部只能有一个非终结符

    • 3型文法（正规文法）

      • 形如 $ A \rightarrow aB 、A \rightarrow a，A,B\in V_N;a \in V_T^* $
      • 左递归

  • 文法实用限制

    • 多余规则：推导中无法用到的规则，有两种情况：

      • 不可达：一个非终结符不在任何规则右部出现
      • 不可终止：一个非终结符不能推导出非终结符来
    • 有害规则：存在例如$ U \rightarrow U $的产生式，对描述语言无必要，会引起文法的二义性

第三章 词法分析

3.1 正规式与正规文法

例如：
$$A=xy: A \rightarrow xB;B \rightarrow y \\ A=x^*y:A \rightarrow xA|y$$
其中冒号左边为正规式，右边为该正规式对应的正规文法

3.2 有穷自动机

练习题

  1. 构造下列正规式的DFA

    1. 1(0|1)*101
    2. 1(1010* | 1(010)*1)*0
    3. a((a | b)* | ab*a)*b
    4. b((ab)* | bb)*ab
  2. 构造一个DFA，它接受$ \sum=\{0,1\} $上所以满足如下条件的字符串：每个1都有0直接跟在右边。然后构造改语言的正规文法。
  3. 将图3.17（a）和（b）中的NFA确定化

第四章 自顶向下的语法分析方法

  • 语法分析常用的两种方法：自顶向下和自底向上的语法分析方法

4.1 LL(1)文法判别

  • 计算FIRST、FOLLOW集得到SELECT集，对于相同左部的产生式的SELECT集之间，若取交集不为空，则该文法不是LL(1)文法，反之则为LL(1)文法。
  • 形式化定义为：一个上下文无关文法是LL(1)文法的充分必要条件是，对每个非终结符A的两个不同产生式，A→α, A→β,满足SELECT(A→α)∩SELECT(A→β)=空集 其中α，β不同时能推导出ε。

4.1.1 SELECT集计算

定义

  • 给定上下文无关文法的产生式A→α， A∈VN，α∈V*, 若α不能推导出ε，则SELECT(A→α)=FIRST(α)
  • 如果α能推导出ε则：SELECT(A→α)=（FIRST(α) –{ε}）∪ FOLLOW(A)
  • 需要注意的是，SELECT集是针对产生式而言的。

4.2 非LL(1)文法转换为LL(1)文法

  • 一个文法若含直接或间接左递归，或含有左公共因子，则该文法肯定不是LL(1)文法。

提取左公共因子

  • 文法中含有$ A \rightarrow \alpha \beta| \alpha \gamma $的产生式时，需要进行等价变换为：

$$ A \rightarrow \alpha A' \\ A' \rightarrow \beta | \gamma $$

4.3 LL(1)分析的实现

4.3.1 递归下降子程序

一般遵照Pascal程序结构设计，例如：

PROCEDURE S;
BEGIN;
    E;T;
END;

PROCEDURE E;
BEGIN;
    IF SYM='a' THEN
        ADVANCE;
    ELSE IF SYM=',' THEN
        ADVANCE;
    ELSE IF SYM='(' THEN
        ADVANCE;
        T;
    IF SYM = ')' THEN
        ADVANCE;
    ELSE
        ERROR;
    ELSE
        ERROR;
END;

4.3.2 预测分析法

构建预测分析表

  • 对文法G[S]的每个产生式$ A \rightarrow \alpha $，执行：

(1) 对每个$ a \in SELECT(A \rightarrow \alpha) $，将$ A \rightarrow \alpha $加入M[A,a]
(2) 所有无定义（完成第一步后空着的）M[A,a]标上出错标记

例

a^(),#
S->a->^->(T)
T->ST'->ST'->ST'
T' ->ε->,ST'

使用预测分析表进行分析

步骤分析栈剩余输入串动作
1#S(a,a)#S->(T)
2#)T((a,a)#'('匹配
3#)Ta,a)#T->ST'
............

第五章 自底向上优先分析

  • 自底向上的分析方法有两种：算符优先分析和LR分析法

5.1 移进-规约

例：有文法G[S]

$$ S→ aAcBe \\ A → b \\ A → Ab \\B → d $$

其分析过程如下：


5.2 算符优先分析

5.2.1 优先关系定义

（1）当文法中存在产生式$ A\rightarrow ...ab... $ 或 $ A \rightarrow ...aBb... $，则a和b的优先级相等
（2）当文法中存在产生式$ A \rightarrow ...aB... $，则对每一个$ b\in FIRSTVT(B) $都有$ a\lessdot b $
（3）当文法中存在产生式$ A \rightarrow ...Bb... $，则对每一个$ a \in LASTVT(B) $都有$ a\gtrdot b $

  • 在算符优先文法中，优先关系仅在终结符之间。

5.2.2 算符优先关系表和分析

  • 算符优先文法：文法G的任一产生式中不含相邻的非终结符
  • 构造算符优先关系表，先扩展文法(S'->#S#)，接着需要先求FIRSTVT集合LASTVT集，可以看成是对于每个产生式右部，若同时有非终结符和终结符，则去除非终结符以后求FIRST或LAST集；若仅有非终结符串A，再考虑求FIRSTVT(A)或LASTVT(A)
  • 算符优先分析：
步骤符号栈优先关系当前符号剩余输入串动作
1#$ \lessdot $(a,a)#移进
2#($ \lessdot $a,a)#移进
3#(a$ \gtrdot $,a)#规约 S->a
4#(S$ \lessdot $,a)#移进
..................

第六章 LR分析

6.1 LR文法间的关系

常用的LR文法有：LR(0)，SLR(1)、LALR(1)、LR(1)
其包含关系结构如图：


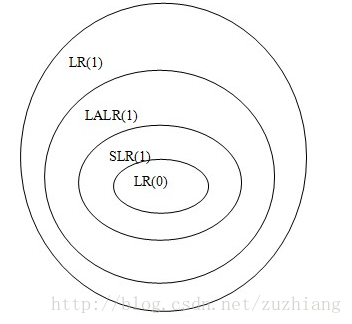
一个文法G[S]，若列出LR(0)项目集规范族C后，C中没有项目集中有移进-规约冲突，那么该文法G[S]就是LR(0)文法。
同时，一个LR(0)文法也是SLR(1)、LALR(1)和LR(1)文法，因为不会再产生新的移进-规约冲突。

6.2 LR文法的判定

6.2.1 LR(0)

一个文法G[S]，若列出LR(0)项目集规范族C后，C中没有项目集中有移进-规约冲突，那么该文法G[S]就是LR(0)文法。
​

项目集和项目集规范族

项目集是一个包含一个或多个项目的集合。LR(0)项目形如：$ I_k=\{S \rightarrow ·\alpha\} $

特别地，对文法G[S]的拓宽文法G[S']：
$ I_0=\{S' \rightarrow ·S,...\} $
若G[S]中有产生式$ A \rightarrow\varepsilon $ 那么这个产生式对应的项目只有$ A \rightarrow· $
这种情况直接对应动作为规约
​

一个例子
有文法G[S]如下：
$$S \rightarrow AS | \varepsilon \\ A \rightarrow aA|b$$
则其拓宽文法G[S']为
$$S' \rightarrow S \\ S \rightarrow AS | \varepsilon \\ A \rightarrow aA|b$$
其项目集有
$$ I_0: \\ S' \rightarrow ·S \\ S \rightarrow ·AS \\ S \rightarrow · \\ A \rightarrow ·aA \\ A \rightarrow ·b $$

$$ I_1：\\ S' \rightarrow S·$$
等等

移进-规约冲突

如上例所示
其项目集I0中有移进-规约冲突：$$ S \rightarrow · \\ A \rightarrow ·aA \\ A \rightarrow ·b $$
对于$ S \rightarrow· $ 应当规约r2；
对于$ A \rightarrow ·aA $和$ A \rightarrow ·b $ 均应当移进。

6.2.2 SLR(1)

这里千万别考。

6.2.3 LALR(1)

LALR(1)的项目集族是建立在LR(1)基础上，合并同心项后不含冲突的新项目集族。
​

同心集

同心集是一种LR(1)中项目集与项目集之间的关系，一般是两个一组互为同心集。同为一组的同心集中的各个项目集中，各个项目一一对应相同，只有项目后的搜索符不同。
​

一个例子
例如：
$$ I_4: B \rightarrow b·,a/b $$
$$ I_7: B \rightarrow b·,\# $$
就是一对同心集
​

合并同心集

将同心集中对应的同心项的搜索符合并（以斜杠/分开）
如上例中的I4和I7合并后为：
$$I_4,I_7: B \rightarrow b·,a/b/\#$$

由LR(1)文法的项目集族合并同心集而来的新项目集族不会产生新的移进-规约冲突，但有可能产生规约-规约冲突。
​

规约-规约冲突

一种冲突，应该不考。

6.2.4 LR(1)

构造LR(1)项目集族，不含冲突便是LR(1)。
​

搜索符

  1. 有项目$ S \rightarrow \alpha ·X \beta ,y $ 和产生式$ X \rightarrow \gamma Z \delta $则在其所在的项目集中:

$$ I_k: \\ S \rightarrow \alpha ·X \beta ,y \\ X \rightarrow · \gamma Z \delta ,z_1/z_2/.../z_n $$
其中$ z_n \in FIRST( \beta y) $

  1. 规定$ S' \rightarrow ·S,\#$则有次产生的左部为S的产生式对应的项目，其搜索符为$ FIRST(\varepsilon \#)=\{\#\} $

LR(1)分析表

例如

状态ACTION GOTO
ab#AS
0S3S4r221
1 acc
2S3S4r225
3S3S4 6
4r4r4r4
5 r1
6r3r3r3
  • 其中ACTION项目下，在对应状态遇到终结符时执行对应动作。Sn指跳转到状态n；rm指使用第m个产生式规约；
  • 在GOTO项目下的数字，代表在对应状态遇到非终结符所要跳转到的状态序号。

LR(1)分析过程

文法G[S]：
$$ S' \rightarrow S \\ S \rightarrow AS| \varepsilon \\ A \rightarrow aA|b $$
分析串abab#

第七章 语法制导的语义计算

例：
给定文法G[S]:
$$S \rightarrow (L) | a \\ L \rightarrow L,S|S $$
其属性文法（翻译模式）如下：

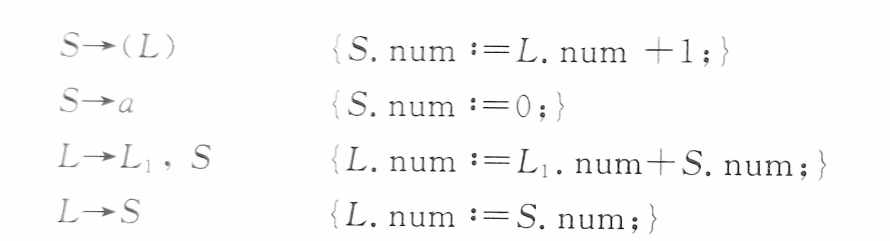
其LR分析表和分析求值过程如下：

第八章 静态语义分析和中间代码生成

8.1 符号表

  • 符号表是编译程序用到的最重要的数据结构之一

  • 符号表中通常存放：

    • 符号的名字
    • 符号的类别（常量、变量、函数名、类名等）
    • 符号的数据类型
    • 符号的存储类别和存储分配信息
    • 符号的作用域和可见性
    • 其它属性

8.1.1 作用域与单符号表组织

8.2 中间代码生成

  • 常见的中间代码表示：

    • 抽象语法树（简称语法树）及其改进有向无圈图DAG
    • 三地址式/四元式
    • P-code（Pascal专用）
    • Bytecode（Java专用）
    • SSA

8.2.1 三地址式/四元式

例：
$$T_7=A+(B*(C-D))+\frac{E}{(C-D)^N}$$

表示为三地址式/四元式：

8.2.2 后缀式（逆波兰式）

  • 对一个式子，画出语法树，后序遍历（最终结果要注意顺序）
  • 遍历语法树时的简单记法：左右根

例
下图语法树(a)的逆波兰式为：ABCD-*ECD-N^/++

第九章 运行时存储组织

  • 运行时存储分配方案有两种：

    • 静态存储分配

    • 动态存储分配

      • 堆式动态存储分配
      • 栈式动态存储分配

第十章 代码优化和目标代码生成

  • DAG化简

  • 目标代码生成技术的三个核心问题：

    • 指令选择
    • 寄存器分配
    • 指令调度

添加新评论

Copyright © 2024 蓝里小窝
Powered by Typecho | Theme by Waxy | 粤ICP备2021091273号 | 粤公网安备 44031102000629号